General

This implementation of the cubic scaling GWR algorithm takes advantage of well-established HPC libraries. More specifically, all the two-point functions are distributed with PBLAS and the diagonalization of the Kohn-Sham as well as the inversion of the dielectric matrix can be performed either with Scalapack or ELPA.

Different kinds of self-consistency have been implemented: from the simplest one-shot GW method to the more involved energy-only self-consistency in which one can update the quasiparticle energies either in the screened interaction or in the Green’s function entering the self-energy or in both. RPA total energies for solids can be computed as well starting from the polarizability in Fourier space and imaginary domain.

At present the GWR code in ABINIT supports norm-conserving pseudopotentials only. The equations needed to generalize the implementation to support the projector-augmented wave method (PAW) are well known and all these terms can be computed using the low-level routines provided by the LibPAW library.

Benchmark

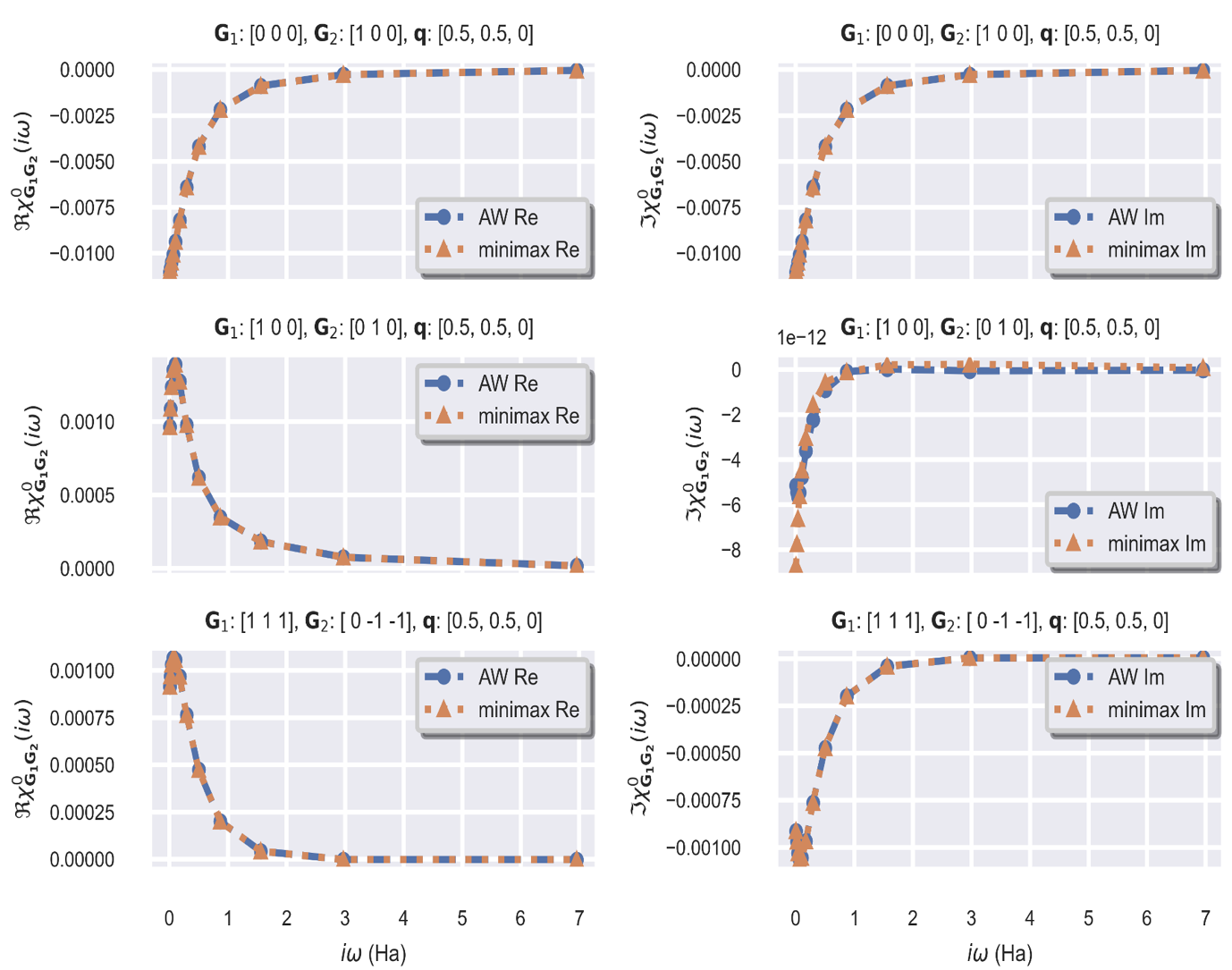
Comparison between susceptibility of silicon calculated using Adler-Wiser formula (blue) and the real space imaginary-time minimax method (orange), with excellent agreement. The left column shows the real part of the susceptibility, and the right column shows the imaginary part of the susceptibility. Note the vertical scale of the middle right figure, that is to be multiplied by the indicated \(10^{-12}\) factor.